Home > Foundation > MOI

Moment of Inertia (MOI)

Any object that is rotating has a tendency to maintain its current state of angular motion (i.e. angular inertia) and moment of inertia (MOI) is the measure of object's angular inertia. Unlike its linear counterpart, MOI does not stay constant as it is a function of the location of the axis of rotation. Figure 1 shows a mass particle, a small mass whose volume effect can be ignored, rotating around an axis. MOI of a mass particle is proportional to its mass and 'square' of the distance from the axis. In other words, the location of the mass particle relative to the axis affects the MOI substantially. It is obvous from Figure 1 that the MOI of the mass particle changes as the distance from the axis changes.

Figure 1. MOI of a mass particale rotating around an axis of rotation. Its MOI (I) is mass (m) times square of the distance from the axis (d).

MOI of an object is more complex than that of a mass particle. An object can be considered as a set of mass particles and its MOI is the sum of the MOIs of individial mass particles composing the object. Figure 2 shows a club rotating about an axis of rotation that passes through the mid section of the grip. The MOI of the club is determined by the mass distribution relative to the axis of rotation. The clubhead has a large mass component located fartheset away from the axis of rotation, which makes the club's MOI large. If the object is rigid with a simple geometric shape its MOI can be computed with the equation shown in Figure 2. The MOI of an irregular but rigid object can be measured directly using an oscillation-based method.

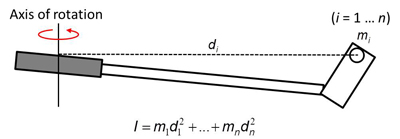
Figure 2. MOI of a club about an axis of rotation that passes through the grip. The club can be considered as a group of mass particles and its MOI is the sum of the MOIs of individual mass particles composing the club. n is the number of particles. Mass distribution within the object relative to the axis of rotation directly affects the object's MOI.

Figure 3 shows how club's MOI changes as the axis of rotation moves. Club's MOI is the smallest when the axis of rotation passes through the center of mass (COM): 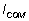. As the axis of rotation moves away from the COM, the MOI increases as a function of the distance from the COM: 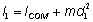, where m is club's mass. The farther the axis moves the larger the MOI becomes. As a result, the club has a larger MOI when it is held at and rotated about the grip (Position 1 in Figure 3) than at the the neck (Position 2) simply because of the distance from the COM. This is called the parallel-axis theorem. This theorem shows well that MOI is determined by object's relative mass distribution about the axis of rotation.

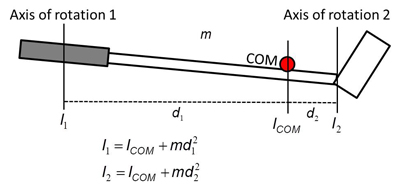
Figure 3. MOIs of the same club about three different parallel axes of rotation. As axis of rotation moves away from the COM, club's MOI increases by mass * square of the distance to the COM.

Figure 4 shows three axes of rotation all passing through the COM of the club but in different directions. Club's MOI about the long axis (shaft axis) is a lot smaller than those about the axes perpendicular to the shaft due to a substantially more compact mass distribution about (or dispersion from) the long axis. As a result, it is substantially easier to rotate the club about the shaft than to swing it. In fact, a club's MOI characteristics can be described by the MOIs about these three perpendicular axes that pass through the COM. The 3x3 matrix shown in Figure 4 (I) is called the inertia tensor of the club.

Figure 4. Club's MOIs about three perpendicular axes that pass through the COM. Club's MOI about the shaft is substantially smaller than those about the other two axes as club's mass is distributed more compactly around the shaft axis.

The MOI of the club can be computed about different points depending on the interest. Figure 5 shows the postures of two former PGA Tour players at event EDA. Club's MOI can be assessed not only about its COM or player's hand center but also about the hub (the mid-trunk point). The hub can be viewed as the center of rotation of the upper body (thorax, head, shoulder girdles, arms, and club). The total MOI of the upper body about the hub is the sum of the MOIs of individual upper body segments and the club about the hub. Although the MOIs of the two clubs about club's COM or hand center may not be that different, their MOIs about the hub can be quite different because of the distances from the hub to club's COM. Player 1 on the left maintains a substantially longer club-to-hub distance due to early casting at the beginning of the downswing and his club MOI about the hub should be substantially larger than that of Player 2 at this position. So even if we assume their body postures are similar, Player 1's upper body MOI about the hub should be larger due to the contribution of the club. To quickly accelerate the body angularly in the early phase of downswing it is important to keep the club close to the body and thus keep club's MOI (and the MOI of the entire upper body as well) relatively small at this position.

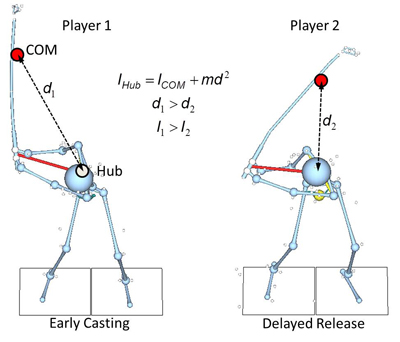
Figure 5. FSP-view postures of two PGA-caliber players at EDA. Player 1's club stays farther from the hub (mid-trunk point) than Player 2 and thus his club MOI about the hub is larger than that of player 2.

Top