Home > Foundation > Mass

Mass

• Inertia and Mass
• Center of Mass (COM)

Inertia and Mass

Inertia is the tendency of matter to maintain its current state of motion: i.e. to remain stationary if it is stationary or to move along a straight path with a constant velocity if it is in motion. Mass, the quantity of matter composing a body, is the measure of inertia in the linear motion. In other words, any object with mass has the tendency to maintain its current state of motion. For example, a puck hit by a hockey stick slides on the ice toward the goal because of its inertia. The state of motion of the puck at the end of the puck-stick contact determines how fast and in which direction it slides. Since the friction between the puck and the ice is small, the puck slides with a pseudo-constant velocity. (If there is no friction, the puck slides with a constant velocity.)

The only way to alter an object's state of motion (i.e. to induce an acceleration) is to exert an external force to the object and inertia can also be defined as the difficulty in changing the state of motion when an external force is acting. In other words, the resulting acceleration is a function of object's inertia (mass). See the Newton's Laws of Motion page for details.

The standard unit (international or SI unit) of mass is 'kg' (kilogram). 'lb' (pound) used in select countries including the US is actually not a unit of mass but of force. lb is used for the gravitational effect of a given mass, not the mass itself. 1 kg is equivalent to about 2.20 lb.

Top

Center of Mass (COM)

Center of mass (COM) of an object is the point about which the object's mass balances in all directions. In the linear motion, it can be assumed that the whole mass is concentrated at this point. When uniform density is assumed, the COM must be on the symmetry lines of the object. For example, Figure 1 shows an elliptical shape whose COM must be at the intersection of the two symmetry lines. When the body is cut through the COM and divided to two sections, both sides should have equal amounts of mass regardless of the orientation of the body (Figure 1).

Figure 1. COM of an object of uniform density with symmetric shape. The COM must be on the symmtry lines and the common intersection of the symmetry lines is where the COM is located. When the object is divided into two sections through the COM, both parts have the same masses as the COM is the balance point of the body.

For an object of fixed irregular shape (with no apparent symmetry), the simplest way to locate the COM is the so-called suspension method in which the object is suspended from two different points. For example, Figure 2 shows a cardboard figure in the shape of a golfer in action suspended from two different points. The COM is located at the intersection of the vertical lines drawn from the suspension point in each position. Again, this method is based on the fact that the COM is the balance point of the object.

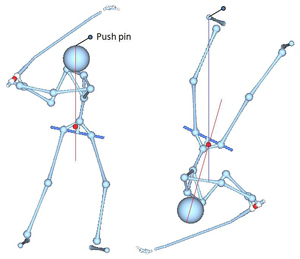
Figure 2. The suspension method of COM location. The object is suspended from two different points (using push pins). The intersection of the two vertical lines drawn from the push pin position in each position is where the COM is located.

The COM can be located either inside or outside the object depending on its shape and mass distribution. For example, the COM of a golf club lies outside the club due to its crooked shape (Figure 3). Because of the relatively large clubhead mass, the COM is located closer to the clubhead. For a rigid object (i.e. golf ball) whose shape and mass distribution do not change, the position of the COM within the body remains the same (Figure 3). When the ball is in contact with the clubhead, however, ball's mass distribution changes due to the deformation. During a golf swing, golfer's body posture changes continuously as the swing progresses and the COM position also changes continuously (dark green line along which golfer's body COM moves; Figure 3).

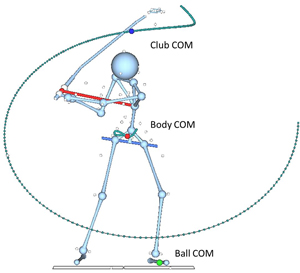
Figure 3. COMs of golfer's body (red ball), club (blue ball), and the ball (green ball). Ball's COM is located inside the ball at the volume center due to its symmetric shape. Club's COM is located outside the cub due to its croked shape and its location changes slightly as the shaft deforms during the swing. Golfer's posture changes continuously and so does the location of his COM.

Since golfer's body posture keeps changing, any fixed shape-based methods (including the suspension method) are not applicable. In biomechanics, golfer's body is typically modeled as a system of rigid segments linked through the joints. (Although the body segments are not rigid, we assume the shapes and mass distributions of the segments remain the same during the action.) In this case, the whole body COM can be computed with the so-called segmental method. The segmental method uses the COM positions of individual segments and their masses in the calculation of the whole body COM location (Figure 4):

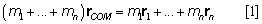
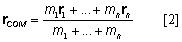
where m is mass, r is position vector, and n is the number of segments included in the body. If it is golfer's body alone, n is 16. If the club is included, n is 17 (Figure 4). If the COM of a body part such as upper lever (thorax + head + arms) is to be computed, n is fewer than 16.

Figure 4. The segmental method of body COM location. Blue dots are the COMs of individual segments while the red dot is the whole body COM. In this model, the body is modeled as a system of 17 rigid segments: hands, forearms, upperarms, feet, shanks, thighs, pelvis, abdomen, thorax, head, and club. Masses and COM positions of the segments are used in the computation of the whole body COM position in this method.

Equation 2 can be applied to each component of the position vector:

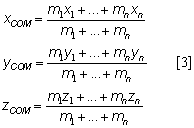
As shown in Equation 3, the position of the whole body COM is essentially a weighted mean of the segmental COM positions with the segmental masses used as weights. Segmental mass values are available in the form of percentages of the whole body mass. For example, the ratios of the segmental masses to the whole body mass reported by De Leva (1978) are listed in Table 1.

Positions of the COMs within individual segments from respective proximal ends are also available in the form of ratios to the segment length (Table 2). The actual COM positions of the segments can be computed from their end point positions and the COM ratios.

The COM position of a segment is a weighted mean of the positions of segment's proximal and distal ends:

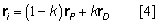
where P is proximal end, D is distal end, and k is the proximal end-to-COM ratio of the segment of interest (i). As a part of motion analysis, the end point coordinates are computed from the markers placed on the body and the segmental COM positions are computed from the end point coordinates.

The location of club COM is determined by the relative masses of the clubhead, shaft, and grip. For the same clubhead, a lighter shaft gives a more distal COM location. The location of the clubhead COM also affects the location of the club COM.

Top

References

• De Leva, P. (1996). Adjustments to Zatsiorsky-Seluyanov's segment inertia parameters. Journal of Biomechanics, 29, 1223-1230.

Top